「排序法」的解題技巧：泡泡排序等經典排序法

本文章會介紹些經典的排序法，比較進階如堆積排序（Heap Sort） 、希爾排序（Shell Sort）等則可先見參考資料。

每種排序法會列出時間複雜度和空間複雜度，此處說明可見 時間/空間複雜度的簡介與實例 一文。

1. 選擇排序法（Selection Sort）
   • 找到最小值，移到最左邊
2. 泡沫排序法（Bubble Sort）
   • 跟隔壁互相比較順序錯了就交換，順序對了就接棒繼續到最後排好一個，再從頭開始
3. 插入排序法（Insertion Sort）
   • 一個一個照順序插入到順序對的位置，最後一次插到對的地方剛好整個排好
4. 合併排序法（Merge Sort）
   • 重複切一半到最小，重複排好左邊排好右邊再合併
5. 快速排序法（Quick Sort）
   • 隨機找一數調整到左邊元素都比它小右邊元素都比他大，左右再重複操作

一、動畫展示各排序法邏輯

1. 選擇排序法/圖片來源: SelectionSort

2. 泡沫排序法/圖片來源: wiki/BubbleSort

3. 插入排序法/圖片來源: wiki/InsertSort

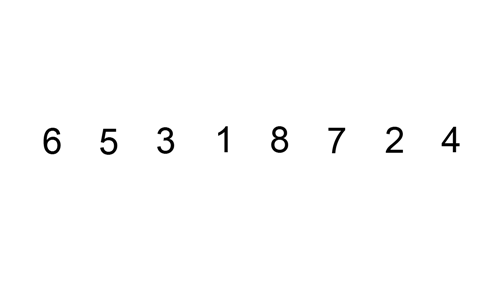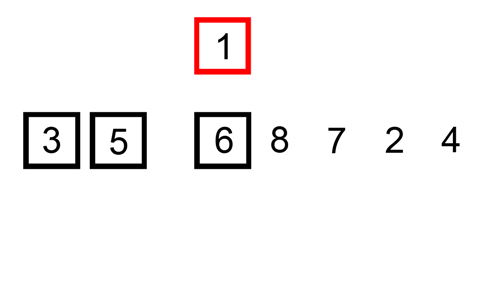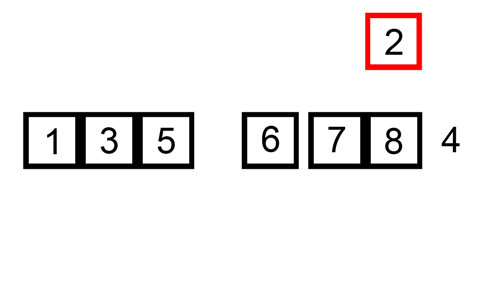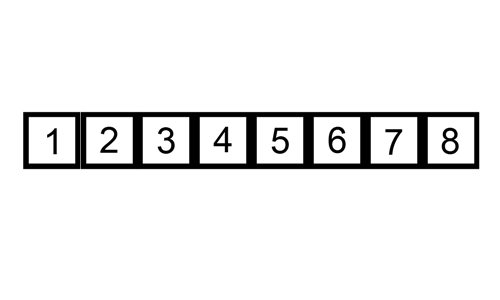
4. 合併排序法/圖片來源: wiki/MergeSort

5. 快速排序法/圖片來源: wiki/Quicksort

二、選擇排序法

1. 時間複雜度: O(n^2)
2. 空間複雜度: O(1)

const selectionSort = (arr) => {
  const length = arr.length;
  for (let i = 0; i < length; i++) {
    let min = arr[i];
    let minIndex = i;
    for (let j = i; j < length; j++) {
      if (arr[j] < min) {
        min = arr[j];
        minIndex = j;
      }
    }  
    // ES6 的用法，交換兩個數值
    [arr[minIndex], arr[i]] = [arr[i], arr[minIndex]];
  }
  return arr;
}

let arr = [1, 3, 5, 7, 2, 4, 8 ,9]
selectionSort(arr) //  [1, 2, 3, 4, 5, 7, 8, 9]

三、泡沫排序法

稱為「泡沫」排序法，因為元素很像「浮」了上來

1. 時間複雜度
   • 平均時間複雜度: O(n^2)
   • 最壞時間複雜度: O(n^2)
   • 最優時間複雜度: O(n)
2. 空間複雜度: O(1)

加上 swapped，如果輸入是已經排好的陣列就只會跑一次內圈，然後就跳掉了，單純跑完一輪不改動，所以時間複雜度會是O(n)。

const bubbleSort = (arr) => {
  const  n = arr.length;
  let swapped = true;  
  for (let i = 0; i < n && swapped; i++) {
    swapped = false;
    for (let j = 0; j < n - 1 - i; j++) {
      if (arr[j] > arr[j + 1]) {
        swapped = true;
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
      }
    }
  }
  return arr;
}

let arr = [1, 3, 5, 7, 2, 4, 8 ,9]
bubbleSort(arr) //  [1, 2, 3, 4, 5, 7, 8, 9]

四、插入排序法

1. 時間複雜度
   • 平均時間複雜度: O(n^2)
   • 最壞時間複雜度: O(n^2)
   • 最優時間複雜度: O(n)
2. 空間複雜度: O(1)

已經排好的陣列，裡面的while只要跑一次就會結束了，就時間複雜度會是O(n)。

const insertionSort = (arr) => {
  const n = arr.length;
  for (let i = 1; i < n; i++) {
    let position = i;
    const target = arr[i];
    while (i >= 0 && arr[position - 1] > target) {
      [arr[position], arr[position - 1]] = [arr[position - 1], arr[position]];
      position--;
    }
  }
  return arr;
}

let arr = [1, 3, 5, 7, 2, 4, 8 ,9]
insertionSort(arr) //  [1, 2, 3, 4, 5, 7, 8, 9]

五、合併排序法

1. 時間複雜度: O(nlogn)
2. 空間複雜度: O(n)

合併排序法要用到遞迴的概念挺為複雜，但在時間複雜度上優於其他排序方式，此處先記錄最簡單能理解的解法，請搭配動畫理解。

const mergeSort =  (arr) => {
  // 合併
  const sortBeforeMerge =  (arr1, arr2) => {
    let sortedArr = []
    while (arr1.length && arr2.length) {
      let minElement = (arr1[0] < arr2[0]) ? arr1.shift() : arr2.shift()
      sortedArr.push(minElement)
    }
    sortedArr = arr1.length ? sortedArr.concat(arr1) : sortedArr.concat(arr2)
    return sortedArr
  }
  // 分割 
  if (arr.length <= 1) {
    return arr
  }
  let middleIndex = Math.floor(arr.length / 2)
  let firstHalf = arr.slice(0, middleIndex)
  let secondHalf = arr.slice(middleIndex)
  return sortBeforeMerge(mergeSort(firstHalf), mergeSort(secondHalf))
}

let arr = [1, 3, 5, 7, 2, 4, 8 ,9]
mergeSort(arr) //  [1, 2, 3, 4, 5, 7, 8, 9]

六、快速排序法

• 時間複雜度
  • 平均時間複雜度: O(nlogn)
  • 最壞時間複雜度: O(n2)
  • 最優時間複雜度: O(nlogn)
• 空間複雜度為：根據實現的方式不同而不同

此處先記錄最簡單能理解的解法，請搭配動畫理解。

function quickSort(arr) {
  if (arr.length <= 1 ) {
    return arr
  }
  let pivot = arr[arr.length -1]
  let left = []
  let right = []
  for(let i = 0; i < arr.length - 1; i++) {
    if (arr[i] < pivot) {
      left.push(arr[i])
    } else {
      right.push(arr[i])
    }
  }
  return [...quickSort(left), pivot, ...quickSort(right)]
}


let arr = [1, 3, 5, 7, 2, 4, 8 ,9]
quickSort(arr) //  [1, 2, 3, 4, 5, 7, 8, 9]

資料來源:一起用 JavaScript 來複習經典排序法吧！演算法 合併排序法（Merge Sort）竹白記事本/排序演算法排序之快速排序法 (Quick Sort)